Programming Basics Prep
Most of the concepts on this page is taken from : Data Structures and Algorithms in Java by Robert Lafore
This is a basic programming concept anyone must know. I will keep this page updated with new code when I have time.
Linear Search vs Binary Search
Linear Search searches for each item in a list. For ordered, average number of steps needed to find an item is N/2. For unordered, average number of steps needed to find an item is N.
Binary Search is like a Guess-a-number game where it checks for value in the middle and see if the number is less or more or equal to that middle number thereby shortening the number of guesses. This can an be applied only to a sorted list.
Guess a number between 1-100 (number 33 guessed)
| Step Number | Number Guessed | Result | Range of Possible Values |
| 0 | 1-100 | ||
| 1 | 50 | Too High | 1-49 |
| 2 | 25 | Too Low | 26-49 |
| 3 | 37 | Too High | 26-36 |
| 4 | 31 | Too Low | 32-36 |
| 5 | 34 | Too High | 32-33 |
| 6 | 32 | Too Low | 33-33 |
| 7 | 33 | Correct |
Binary search provides a significant speed increase over a linear search. If we used linear search it would have took us 33 guesses but in binary search it only took us 7. For small number of items it is not significant but for large items binary is way more faster than linear.
Logarithms
Comparisions needed in Binary Search
10 -> 4, 100 -> 7, 1000 -> 10, 10,000 -> 14 and so on…
| Steps s | Range r | Range expressed as power of 2 |
| 0 | 1 | 2^0 |
| 1 | 2 | 2^1 |
| 2 | 4 | 2^2 |
| 3 | 8 | 2^3 |
| 4 | 16 | 2^4 |
| 5 | 32 | 2^5 |
| 6 | 64 | 2^6 |
| 7 | 128 | 2^7 |
As we can see 7 steps cover the range of 100 (128 in total).
Doubling the range each time creates a series that’s the same as raising two to a power. We can express this power as a formula. If s represents the steps and r represents the range, the equation is
r = 2^s
(eg. 128 = 2^7)
The inverse of raising something to the power is logarithm. This equation says that the number of steps (comparisions) is equal to the logarithm to the base 2 of the range.
s = log2(r)
It is usually log to the base 10 but we can convert easily to base 2 by multiplying by 3.322
[ex. log10(100) = 2, log1(100) = 2*3.322, which is equal to 6.644 (approx. 7)]
Big O Notation
Big O Notation is used to measure how efficient a computer algorithm is.
T is time, K is constant
Insertion in unordered array : T = K (Insertion requires a same amount of time no matter how big is the arrray)
Linear Search: T = K * N/2 (The number of comparisions that must be made to find a specified item is, on average, half of the total number of items) We can combine constant with 2 and the new formula is T = K*N where K is the new constant.
Big O Notation dispenses with the constant K. All we want to compare is how T change for different values of N, not what the actual numbers are.
We read O(1) as the order of 1.
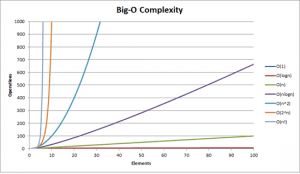
Therefore we can say, Linear Search takes O(N) time and Binary Search takes O(log N) time. Insertion into unordered array takes O(1) or constant time which is ideal!
| Algorithm | Running Time in Big O |
| Linear Search | O(N) |
| Binary Search | O(log N) |
| Insertion in unordered array | O(1) |
| Insertion in ordered array | O(N) |
| Deletion in unordered array | O(N) |
| Deletion in ordered array | O(N) |
O(1) is excellent, O(log N) is good, O(N) is fair, O(N^2) is poor. Bubble sort is O(N^2).
Simple Sorting
Bubble Sort
It is simplest of the sorting algorithms and very slow. You start at the left end of the list and compare the two values in index 0 and 1. If value in 0 is greater than a value in 1 then we swap the positions. If value in 0 is smaller than value in 1 we don’t do anything. We then move over one position and compare values in index 1 and index 2. We do this until all the values are sorted. As the algorithm progresses, the biggest items “bubble up” to the top end of the array. After this first pass through all the data, we’ve made N-1 comparisions and somewhere between 0 and N-1 swaps.
Now, we go back again and start another pass from left end of the array towards the right. However, we stop at N-2 because we know N-1 already contains largest number. On each external iteration/pass we decrease the size of N.
for(int i =array.length-1; i>1; i--){
for(int j =0; j<= array.length; j++){
//swap if needed
if(array[j] > array[j+1]{
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}Efficiency of Bubble Sort
In general, where N is the number of items in the array, there are N-1 comparisons on the first pass, N-2 on the second and so on…
(N-1)+(N-2)+(N-3)+…+1 = N*(N-1)/2
Thus, the algorithm makes about N^2/2 comparisions as we get rid of -1 as it makes no difference. We know if data is random, a swap is necessay about half the time on average so there will be N^2/2 * 1/2 = N^2/4 swaps. We can ignore the constant 2 (or 4) thus it gives us the Big O Notation of O(N^2) which is very poor.
Selection Sort
This sort reduces the number of swaps necessary from O(N^2) as in bubble sort to O(N). Unfortunately, the number of comparisions remains the same O(N^2).
In this type of sorting, we look for the lowest number in the list and swap it with the index 0 of the one on the left. We then start again from index 1 and look for the lowest number and swap it with the value in index 1. We continue forward until we reach the index N-1. In this algorithm the sorted numbers accumulate on the left side.
int minVal;
for(int i = 0; i<array.length-1; i++){
minVal = i;
for(int j = i+1; j<array.length; j++){
if(array[j]<array[minVal]){
minVal = j;
int temp = array[i];
array[i] = array[minVal];
array[minVal] = temp;
}
}
}Efficiency of Selection Sort
Selection sort performs the same number of comparisions as the bubble sort N*(N-1)/2. But, it is faster because there are so few swaps. For smaller values of N, hte selection sort may in fact be much faster than bubble sort. For large values of N, the comparision times will dominate, so we would have to say that the selection sort runs in O(N^2) time just as bubble sort.
Insertion Sort
In insertion sort, we divide the unsorted list into two and sort the list on the left (partial sorting). Then we take the value from the start index of the second list, compare it with first list and put the number in appropriate position while shifting remaining numbers from first list to the right. We continue the process until we go through all the numbers in the second list.
int i, j;
for(i = 1; i<array.length; i++){ //i is dividing line
int temp = array[i]; //remove marked item
j = i; //start shifts at i
while(j>0 && array[j-1] >= temp){ //until j is smaller,
array[j] = array[j-1]; //shift item to right
--j; //go left one position
}
array[j] = temp; //insert marked item
}Efficiency of Insertion Sort
On the first pass, it compares the maximum of 1 item. On second pass 2 and so on up to N-1
1 + 2 + 3 + … + N-1 = N*(N-1)/2
On each pass only 1/2 of the maximum number of items are actually compared before the insertion point is found, we can divide by 2. So, N*(N-1)/4
The insertion sort runs in O(N^2) time for random data and when data is almost sorted it runs at O(N).
Stacks and Queues
Stacks and Queues are more restricted and abstract as we can only access one data at a time – either on top or on the bottom. We can use Arrays to understand the concept but we can also use Linked Lists and Heap.
Stacks
A stack allows access to onle one data item: the last item inserted. Think of it as a stack of books on the table. You put a book on top of the stack and, you take a book from the top of the stack. Basically it is Last-In-First-Out(LIFO). Example: Stack can be used to check whether paranthesesm, braces and brackets are balanced in a computer program. In binary trees, it can be used to traverse the nodes of a tree. In Graphs, it can be used to search the vertices of a graph. Most microprocessors use a stack based architecture. When a method is called, its return address and arguments are pushed onto a stack, and when it returns, they are popped off.
public class StackX{
//size of stack array
private int maxSize;
//Array
private int[] stackArray;
//top of stack
private int top;
//put an item on a stack
public void push(int j)
{
stackArray[++top] = j;
}
//take item from top of stack
public int pop(){
return stackArray[top--];
}
//peek at the top of the stack
public int peek()
{
return stackArray[top];
}
//check if stack is empty
public boolean isEmpty()
{
return(top == -1);
}
//check if stack is full
public boolean isFull()
{
return(top==maxSize-1);
}
} // end of StackX class
public class StackApp
{
StackX theStack = new StackX(10); // new stack creation
theStack.push(10);
theStack.push(30); //add values to stack
while(!theStack.isEmpty()) //loop through stack to pop and display
{
int value = theStack.pop();
System.out.println(value);
}
}
Efficiency of Stack : Constant O(1) time and is not dependent on number of items.
Queues
It is a data structure that is somewhat like a stack, except that in a queue the first item inserted is the first item to be removed (First-In-First-Out, FIFO). Example: A queue works as a line in an apple store: first person to stand gets the first iPhone, a printer’s queue when you hit that print command and, typing things on a screen, etc.
Circular queue: when you insert an item in a queue, it sits at the back of the line. And, when you remove an item, the spot is empty at the front. You can push all the values to the front to make up that space but it is somewhat inefficient. So, we just circle through the array or spots.
class Queue{
private int maxSize;
private int[] queArray;
private int front;
private int rear;
private int nItems;
public Queue(int s){
maxSize = s;
queArray = new Int[maxSize];
front = 0;
rear = -1;
nItems = 0;
}
public void insert(int j){
if(rear == (maxSize-1)){
rear = -1;
}
queArray[++rear] = j;
nItems++;
}
public int remove(){
int temp = queArray[front++];
if(front==maxSize){
front=0;
}
nItems--;
return temp;
}
public int peekFront(){
return queArray[front]
}
public boolen isEmpty(){
return (nItems==0);
}
public boolean isFull(){
return (nItems==maxSize);
}
public int size(){
return nItems;
}
}
class QueueApp{
Queue theQueue = new Queue(5);
theQueue.insert(10);
theQueue.insert(30);
theQueue.remove();
theQueue.insert(20);
while(!theQueue.isEmpty()){
int n = theQueue.remove();
System.out.println(n);
}
}
Efficiency of Queues: O(1) time as we insert and remove data
Priority Queues
This is a more specialized form of a queue. Like an ordinary queue, priority queue has a front and a rear, and items are removed from the front. However, in a priority queue, items are ordered by key value so that the item with the lowest key is always at the front. Example: Sorting of letters in order of priorities, minimum spanning trees, weighted graphs.
Efficiency of Priority Queues: Insertion runs in O(N) time as it has to sort the values first. Deletion takes O(1). We can improve insertion time using heaps.
Arrays
Arrays are the most commonly used data structure. But, it is not always ideal. In an unordered array insert takes O(1) time but searching is slow O(N). In ordered array search is quick O(log N) but insertion takes O(N). For both, deletion takes O(N). Linked Lists is another viable option.
- Important things to understand: Insertion, Searching, Deletion
- Average number of steps needed to find and item is N/2 (worst case N)
- A deletion requires searching through an average of N/2 elements and then moving the remaining elements(N/2) to fill up the resulting hole. Total steps is N.
Creating an array:
//initialization
int[] count = new int[3]; //Integer Array of 3 empty slots.
int[] count2 = new int[]{1, 2, 3};
int[] count3 = {1,2,3};
//initialization
String[] arrayString = new String[8]; //String Array of 8 empty slots.
String[] arrayString2 = new String[]{"a","b"};
String[] arrayString3 = {"a","b"};Accessing Array:
int second = count[2]; String third = arrayString[3];
Inserting Values in Array:
count[2] = 4; arrayString[3] = "c";
Some common examples:
Reverse a String
System.out.println(reverseString("Elephant"));
public String reverseString(String key){
String reversedString = "";
for(int i = key.length();i>=0;i--){
reversedString+=key.charAt(i);
}
return reversedString;
}
//Recursion
String reversedString = reverseRec("elephant", "", "elephant".length());
public String reverseRec(String key, String reversed, int i){
if(i<0){
return reversed;
}
reversed = reversed+key.charAt(i);
return reverseRec(key, reversed, i-1);
}
//Output: tnahpelESorting numbers in an Array
//Bubble Sort
int[] sortArray = {2,3,1,7,5,9,10,4,7,9};
for (int i = 0; i < sortArray.length; i++) {
for (int j = i + 1; j < sortArray.length; j++) {
int tmp = 0;
if (sortArray[i] > sortArray[j]) {
tmp = sortArray[i];
sortArray[i] = sortArray[j];
sortArray[j] = tmp;
}
}
System.out.println(sortArray[i]);
}Sum of Numbers in an Array
int[] sortArray = {2,3,1,7,5,9,10,4,7,9};
int sum = 0;
for(int k:sortArray){
sum+=k;
}Fibonacci Series with and without Recursion
//Fibonacci Series
printFibonacci(10, true);//recusrive
printFibonacci(10, false);//non-recursive
static int n1=0,n2=1,n3=0;
static void printFibonacci(int count, boolean recursion){
//using recursion
if(recursion){
if(count>0){
n3=n1+n2;
n1=n2;
n2=n3;
System.out.print(" "+n3);
printFibonacci(count--, true);
}
}else{
//without recursion
System.out.println(n1+" "+n2);
for (int i=2;i<=count;i++){
n3=n1+n2;
n1=n2;
n2=n3;
System.out.print(" "+n3);
}
}
}Check prime number
public boolean findPrime(int value){
boolean isPrime = false;
if(value<2){
isPrime=false;
}else{
isPrime=true;
}
for(int i=2; i<=value/i; i++){
if((value%i)==0){
isPrime = false;
break;
}
}
return isPrime;
}Binary Search
int[] arrayValues = {1,5,8,10,24,35,44,65,76};
int arraySize = arrayValues.length;
boolean checkBinarySearch = binarySearch(10);
public boolean binarySearch(int key){
int low = 0;
int high = arraySize-1;
while(high>=low){
int middle = (low+high)/2;
if(arrayValues[middle]==key){
return true;
}
if(arrayValues[middle]< key){
low=middle+1;
}
if(arrayValues[middle]>key){
high=middle-1;
}
}
return false;
}Linear Search
int[] arrayValues = {1,5,8,10,24,35,44,65,76};
int arraySize = arrayValues.length;
public void linearSearch(int key){
for(int i=0; i<arraySize; i++){
if(arrayValues[i]==key){
System.out.println("Found");
}else if(i==arraySize){
System.out.println("Not Found");
}
}
}Factorial
public static int factorial(int key){
int result = 1;
for(int i=1; i<= key; i++){
result = result* i;
}
return result;
}
public int factorialrec (int key){
int result;
if(key==1){
return 1;
}
result = key*factorialrec(key-1);
return result;
}Palindrome
public boolean checkPalindrome(String key){
int i = 0;
int j = key.length()-1;
while(j>i){
if(key.charAt(i)!=key.charAt(j)){
return false;
}
++i;
--j;
}
return true;
}Shuffle a deck of cards
private static final int DECK_SIZE = 52;
//Using Collections Library
public void randomizeCards(){
ArrayList<Integer> deck = new ArrayList<Integer>();
for (int i = 0; i < DECK_SIZE; ++i) {
deck.add(i);
}
Collections.shuffle(deck);
System.out.println(deck);
}
//Using Arrary List
public void randomizeCardsB(){
ArrayList<Integer> deck = new ArrayList<Integer>();
for (int i = 0; i < DECK_SIZE; ++i) {
deck.add(i);
}
ArrayList<Integer> shuffledDeck = new ArrayList<Integer>();
while (deck.size() > 0) {
int index = (int) (Math.random() * deck.size());
shuffledDeck.add(deck.remove(index));
}
System.out.println(shuffledDeck.toString());
}Check for Anagrams
//check for anagrams
public boolean checkAnagrams(String first, String second){
int lengthf = first.length();
int lengths = second.length();
int j = 0;
if(lengthf==lengths){
char[] charArray1 = first.toCharArray();
char[] charArray2 = second.toCharArray();
Arrays.sort(charArray1);
Arrays.sort(charArray2);
for(int i=0; i<lengthf; i++){
if(charArray1[i]==charArray2[i]){
j++;
}else{
return false;
}
if(lengthf==j){
return true;
}
}
}
return false;
}Find first non repeating char in a string
static final int NO_OF_CHARS = 256;
static char count[] = new char[NO_OF_CHARS];
static void getCharCountArray(String str)
{
for (int i = 0; i < str.length(); i++)
count[str.charAt(i)]++;
}
static int firstNonRepeating(String str)
{
getCharCountArray(str);
int index = -1, i;
for (i = 0; i < str.length(); i++)
{
if (count[str.charAt(i)] == 1)
{
index = i;
break;
}
}
return index;
}
Linked Lists
Arrays have certain disadvantages as data storage structures. In an unordered array, searching is slow, whereas in an ordered array, insertion is slow. In both, deletion is slow. Also, the size of an array can’t be changed after it’s created.
Linked Lists can replace an array as the basis for other storage structures such as stacks and queues. In fact, you can use a linked list in many cases in which you use an array, unless you need frequent random access to individual items using an index.
Links
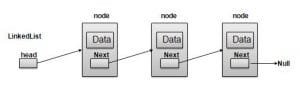
In a linked list, each data item is embedded in a link. A link is an object of a class Link (or something similar). Each link object contains a reference to next link in the list. A field in the list itself contains a reference to the first link. This kind of class definition is sometimes called self-referential because it contains a field (called next) of the same type as itself.
Class Link{
public int iData; //similar to index in array
public int dData; //actual value
//you can also hold an object instead of variable
public objetItem obj;
pubic Link next; //reference to next link
}In Java, a Link object doesn’t really contain another Link object. The next field of type Link is only a reference to another link, not an object.
How Linked List differs from Array
In an array each item occupies a particular position. This position can be directly accessed using an index number.Like a row of houses – once you know the address you know the position. In a List, the only way to find a particular element is to follow along the chain of elements.
A Simple Linked List
- Inserting an item at the beginning of the list
- Deleting the item at the beginning of the list
- Iterating through the list to display contents
class Link
{
public int iData;
public String dData;
public Link next;
public Link(int id, String dd){
iData = id;
dData = dd;
}
public void displayLink(){
System.out.println(iData+" has "+dData);
}
}
class LinkList{
private Link first;
public LinkList(){
first=null;
}
public boolean isEmpty(){
return (first==null);
}
public void insertFirst(int id, String dd){
Link newLink = new Link(id, dd);
newLink.next = first;
first = newLink;
}
public Link deleteFirst(){
Link temp = first;
first = first.next;
return temp;
}
public void displayList(){
Link current = first;
while(current!=null){
current.displayLink();
current = current.next;
}
}
}
class LinkListApp{
public static void main (String[] args){
LinkList theList = new LinkList();
theList.insertFirst(100, "Hello");
theList.insertFirst(101, "World");
theList.displayList();
while(!theList.isEmpty()){ //until the list is empty
Link aLink = theList.deleteFirst();
}
}
}Finding and Deleting Specified Link
public Link find(int key){
Link current = first;
while(current.iData != key){
if(current.next == null){
return null;
}else{
current = current.next;
}
}
return current;
}
public Link delete(int key){
Link current = first;
Link previous = first;
while(current.iData != key){
if(current.next == null){
return null;
}else{
previous = current;
current = current.next;
}
}
if(current == first){
first = first.next;
}else{
previous.next = current.next;
}
return current;
}Double-Ended Lists
A double-ended list is similar to an ordinary linked list, but it has one additional feature: a reference to the last link as well as to the first. The reference to the last link permits you to insert a new link directly at the end of the list as well as at the beginning. You can also do this with Linked List but you will have to traverse through the whole list and then insert it which is inefficient.
Linked List Efficiency: Insertion and deletion at the very beginning of a linked list are very fast – O(1). Finding, deleting, or inserting next to a specific item requires searching through an average of half the items in the list. This requires O(N) comparisions. An array is also O(N) for these operations but linked list is nevertheless faster because nothing needs to be moved when an item is inserted or deleted. Linked List uses exactly as much memory as it needs and can expand to fill all of available memory. The size of an array is fixed (except vector, but is still inefficient).